Before we proceed lets recall..
What are vectors?
Vector is a quantity having a direction and a magnitude.
Example : A car moving east with a velocity V. Here velocity is a vector quantity because it has both magnitude (how fast the car is moving) and direction (east).
Some of the terms/properties we may have learnt from school : magnitude, Vector addition, subtraction, dot product, cross product etc.,
What is an Origin? : Origin is an assumption point from which every other position is referred.
For example if I am the origin and I'm looking at a cat that is 2 meters away from me, then if I assume my position at (0,0) and draw a line towards the cat, the length of the line will be 2 meters.
Warm up example : (vector addition)
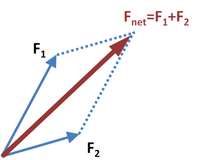
Two forces are acting on a stationary object F1 and F2. Suppose if F1 and F2 are equal, then the resultant direction of the object will be the vector addition of these two forces. How much the object will move can be found using parallelogram law of forces.
Example application 1 : (vector subtraction, magnitude of vector, unit vectors)
Given the Tamil Nadu map with origin at Chennai (we know the exact location of any city from the origin in the given map), find the exact location of Erode with respect to Madurai. (all co-ordinates in kilometers)

By vector property,
Chennai to Erode vector = Chennai to Madurai vector + Madurai to Erode Vector
Madurai to Erode vector = Chennai to Erode Vector - Chennai to Madurai vector
= (-350 i - 220 j) - ( - 214 i - 360 j)
This means that Erode is located 136 kms west and 140 kms north to Madurai.
If we have to compute the distance from Madurai to Erode, we just have to find the magnitude of the vector
distance = sqrt(-136^2 + 140^2) = 195.2 kms
To find the unit vector we have to divide the vector by the distance
Madurai to Erode unit vector = (-136 i + 140 j)/195.2 = - 0.69 i + 0.72 j. If we calculate the magnitude of the unit vector it will be exactly 1.
Now suppose if we have to find the position of that tea stall that is exactly 50 kms in the direction from madurai to erode, we have to multiply 50 with this unit vector
Tea stall position with respect to Madurai = 50 * (-0.69 i + 0.72 j)
i.e. Tea stall is exactly 34.5 Kms west and 36 kms north from Madurai.
In the example we've used 2 dimensional positions.
Suppose we had to compute the distance or position the same way for satellites, planets and galaxies in 3D, we can use the same method.
Example application 2 :
What you can understand : When to use dot product and when to use cross product
Lets assume you design a humanoid robot with a gun. Now suppose you want to program the robot to shoot a balloon you need to know what angle the robot should turn in order to shoot the balloon.
Suppose lets say your robot is stationary at position (0,0) (origin) facing east.
i.e. facing directional vector = i
Now lets say the balloon is at position (6,9).
target unit vector = (6i + 9j) / sqrt(6*6+9*9)
The robot has to turn an angle in the anti clock wise direction until the gun is pointed at position 6,9.
To find this angle you can use dot product..
initial vector . target vector = initial vector * target vector cos Theta
Theta = cos-1 (initial vector . target vector)
= 56.63 degrees
Cross product is usually used when we need a 3rd perpendicular vector (in a 3D space)
Chennai to Erode vector = Chennai to Madurai vector + Madurai to Erode Vector
Madurai to Erode vector = Chennai to Erode Vector - Chennai to Madurai vector
= (-350 i - 220 j) - ( - 214 i - 360 j)
= -136 i + 140 j
This means that Erode is located 136 kms west and 140 kms north to Madurai.
If we have to compute the distance from Madurai to Erode, we just have to find the magnitude of the vector
distance = sqrt(-136^2 + 140^2) = 195.2 kms
To find the unit vector we have to divide the vector by the distance
Madurai to Erode unit vector = (-136 i + 140 j)/195.2 = - 0.69 i + 0.72 j. If we calculate the magnitude of the unit vector it will be exactly 1.
Now suppose if we have to find the position of that tea stall that is exactly 50 kms in the direction from madurai to erode, we have to multiply 50 with this unit vector
Tea stall position with respect to Madurai = 50 * (-0.69 i + 0.72 j)
= -34.5 i + 36j
i.e. Tea stall is exactly 34.5 Kms west and 36 kms north from Madurai.
In the example we've used 2 dimensional positions.
Suppose we had to compute the distance or position the same way for satellites, planets and galaxies in 3D, we can use the same method.
Example application 2 :
What you can understand : When to use dot product and when to use cross product
Lets assume you design a humanoid robot with a gun. Now suppose you want to program the robot to shoot a balloon you need to know what angle the robot should turn in order to shoot the balloon.
Suppose lets say your robot is stationary at position (0,0) (origin) facing east.
i.e. facing directional vector = i
Now lets say the balloon is at position (6,9).
target unit vector = (6i + 9j) / sqrt(6*6+9*9)
= 0.55i + 0.83j
The robot has to turn an angle in the anti clock wise direction until the gun is pointed at position 6,9.
To find this angle you can use dot product..
initial vector . target vector = initial vector * target vector cos Theta
Theta = cos-1 (initial vector . target vector)
= cos-1 (0.55 i + 0.83j . i + 0j)
= cos-1 0.55
= 56.63 degrees
Cross product is usually used when we need a 3rd perpendicular vector (in a 3D space)
Always remember this 2 line rule :
1) Dot product is used to find the angle between two vectors
2) Cross product is used in case of 3D when we need to find how much a vector is tilted from each axis.
Cross product is also applied when we find angular momentum, Torque etc.,
Example application 3 :
Vector physics
From the above problem you have found the angle your robot has to rotate to shoot the balloon. Now assume the bullet is traveling from the gun towards the balloon and you need to find the position of the bullet after 0.5 seconds after you shoot.
Bullet position = Gun position + velocity vector of the bullet * T
The same principle is used if you need to find the position of a rocket when a rocket is launched in space. Note that friction, gravity and other external factors should also be considered. In vacuum, we can safely assume that there are no external factors.
Few more :
1) Vectors are used in every game you play. So if you want to create games, you've to be strong in vector algebra.
2) 3D glasses / VR glasses project 2 different 2D images. It appears 3D because of a hack called Depth Vector! Our naked eyes is capable to see things on 3D because it knows how far is every pixel/color of an object is. This is exactly what is projected in the two images (distance from left eye in the left eye image, distance from right eye in the right eye image)
1) Dot product is used to find the angle between two vectors
2) Cross product is used in case of 3D when we need to find how much a vector is tilted from each axis.
Cross product is also applied when we find angular momentum, Torque etc.,
Example application 3 :
Vector physics
From the above problem you have found the angle your robot has to rotate to shoot the balloon. Now assume the bullet is traveling from the gun towards the balloon and you need to find the position of the bullet after 0.5 seconds after you shoot.
Bullet position = Gun position + velocity vector of the bullet * T
The same principle is used if you need to find the position of a rocket when a rocket is launched in space. Note that friction, gravity and other external factors should also be considered. In vacuum, we can safely assume that there are no external factors.
Few more :
1) Vectors are used in every game you play. So if you want to create games, you've to be strong in vector algebra.
2) 3D glasses / VR glasses project 2 different 2D images. It appears 3D because of a hack called Depth Vector! Our naked eyes is capable to see things on 3D because it knows how far is every pixel/color of an object is. This is exactly what is projected in the two images (distance from left eye in the left eye image, distance from right eye in the right eye image)

